Cos'è e come funziona
Il TT Coumba Freide Tennistavolo ha istituito in maniera sperimentale un sistema di ranking interno per i propri soci, ricavato sulla base del sistema ELO.
Il sistema prende il nome dal matematico professore di fisica statunitense di origine ungherese Arpad Emrick Elo che lo inventò per misurare la forza relativa di un giocatore rispetto agli altri.
Il sistema è così famoso da essere adottato, oltre che dalla federazione degli scacchi, da innumerevoli altre discipline sportive e non, magari solo modificato o perfezionato per esigenze particolari, ma sempre secondo la logica di funzionamento del sistema originario. Lo stesso ranking ufficiale adottato dalla F.I.Te.T. è derivato dal sistema ELO.
Il presupposto matematico che sta alla base del sistema e ne garantisce il funzionamento è che il ranking di un giocatore non viene calcolato in maniera assoluta (cosa peraltro praticamente impossibile non esistendo criteri oggettivi di valutazione) ma viene calcolato sulla base dei risultati ottenuti in partite ufficiali tenendo conto del ranking dell’avversario.
In pratica ciò significa che la variazione di punti che scaturisce dopo una partita ufficiale giocata dipende ovviamente dal risultato ottenuto ma l’entità della variazione è collegata alla differenza iniziale di ranking dei due giocator, la quale definisce il cosiddetto “risultato atteso” o la probabilità di vittoria che vi era prima di giocare.
Prima di fare un esempio chiarificatore (chi non ama la matematica può direttamente saltare all’esempio sottoriportato) si vogliono enunciare i fondamenti matematici del sistema.
La curva di variazione più utilizzata, che definisce la probabilità di vittoria (o risultato atteso), è la cosiddetta formula logistica. La curva utilizzata dal sistema ELO Coumba è la seguente:
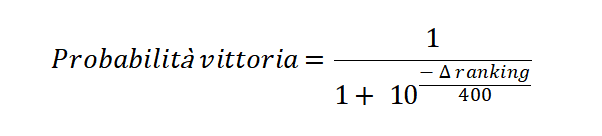
Qui sotto invece il grafico della curva.
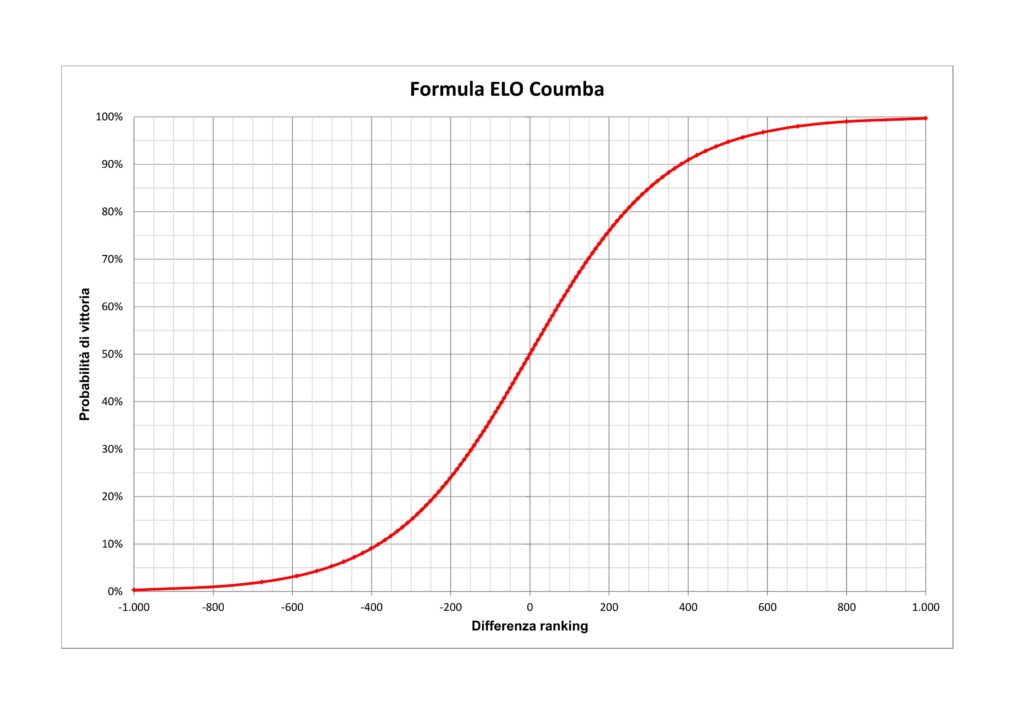
Con una buona approssimazione, la curva può essere rappresentata anche sulla base della tabella sottoriportata:
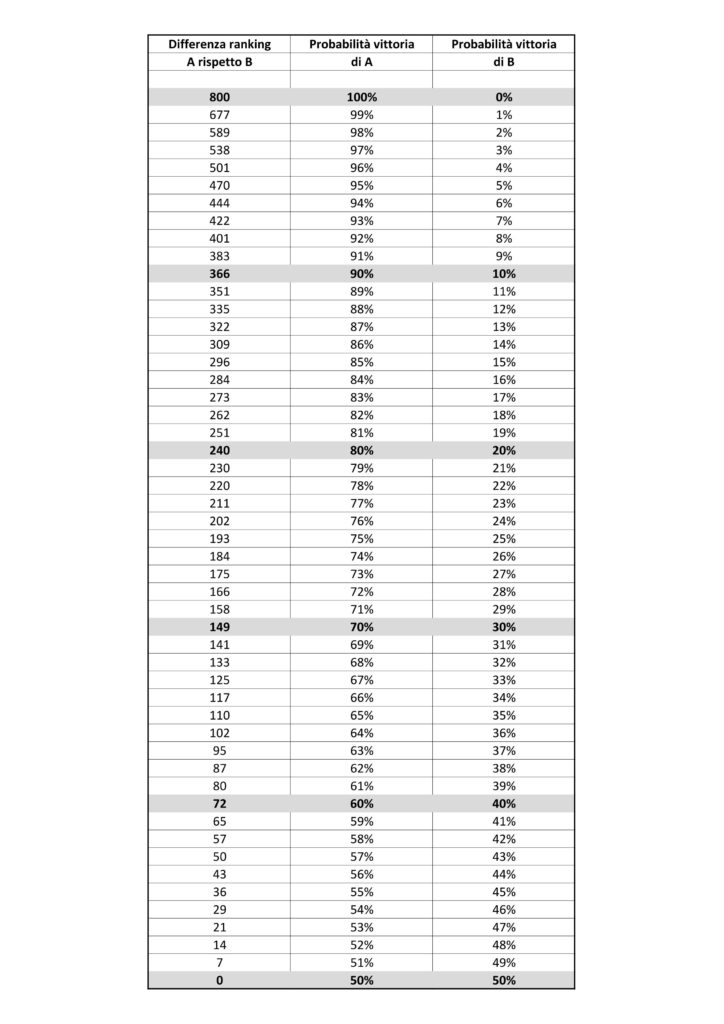
La curva sopra riportata definisce, come detto, la probabilità di vittoria che un giocatore A ha rispetto ad un giocatore B a seconda dei rispettivi ranking e in particolare della loro differenza. Ad esempio una differenza di ranking di 149 punti fra i due giocatori fa prevedere che il giocatore con ranking più alto ha il 70% (0,7 in numero) di possibilità di vittoria mentre l’avversario solo il 30% (0,3).
Al termine dell’incontro disputato tale probabilità di vittoria viene confrontata con il risultato ottenuto. Nel caso di vittoria di A, lo stesso giocatore avrebbe ottenuto un risultato un po’ migliore di quello che ci si poteva aspettare nel senso che la vittoria non era certa (le probabilità erano pari al 70% e non al 100%). Da tale incontro scaturirebbe un lieve incremento di punti di A e il conseguente lieve decremento di B.
Nela caso opposto (vittoria del giocatore B), il giocatore A avrebbe ottenuto un cattivo risultato in quanto era favorito per la vittoria in virtù del suo ranking maggiore. Ciò comporterebbe una forte perdita di punti di A e un altrettanto forte incremento di B che in teoria era sfavorito.
La formula che di fatto regola l’attribuzione dei punteggi in più o in meno è la seguente:
guadagno (o perdita) punti = k * (risultato conseguito – risultato atteso)
dove:
- k è un semplice coefficiente moltiplicativo che definisce il massimo della variazione possibile; matematicamente infatti il massimo punteggio conseguibile in più o in meno è pari a k e nel caso di due giocatori aventi lo stesso livello (stesso ranking) la variazione di punti sarà pari a k/2
- il risultato atteso è quello sopra definito dalla curva (o in maniera approssimata dalla tabella)
- il risultato conseguito è il risultato della partita; nel caso del sistema ELO Coumba il risultato conseguito è quello di cui alla tabella sottostante:
Risultato finale della partita Risultato conseguito
3 set a 0 1
3 set a 1 0,8
3 set a 2 0,6
2 set a 3 0,4
1 set a 3 0,2
0 set a 3 0
Da quanto sopra descritto, si può affermare che Il sistema ELO Coumba è un sistema perfettamente bilanciato nel senso che non sono previsti k differenti per i giocatori e matematicamente i punti guadagnati dal vincitore sono sempre uguali ai punti persi dallo sconfitto. Si può dire quindi che al termine della partita il vincitore “ruba” dei punti allo sconfitto e l’entità della variazione in più o in meno dipende dalla forza relativa (differenza di ranking) dei due giocatori che vi era prima di giocare. Il risultato ottenuto, infine, dipende anche dal numero di set vinti o persi nell’incontro.
A questo punto occorre fare un esempio chiarificatore del sistema ELO Coumba:
Supponiamo che si debba svolgere un incontro tra:
- giocatore A avente punti iniziali pari a 1.200
- giocatore B avente punti iniziali pari a 960
Per prima cosa si deve calcolare la probabilità di vittoria / sconfitta dei due giocatori. Utilizzando la tabella si può vedere che, essendo la differenza di ranking pari a 240 punti (1.200 – 960), la probabilità di vittoria (o risultato atteso) di A è pari all’80% (0,8) mentre la probabilità di vittoria (o risultato atteso) di B è pari al 20% (0,2).
Supponiamo che k vale 20 (nel sistema ELO Coumba questo valore non cambia ed è uguale per tutti i giocatori)
A questo punto viene disputato l’incontro. Vediamo i possibili risultati e come cambia il punteggio di entrambi i giocatori. In particolare si legga la tabella sopra riportata che definisce il “risultato conseguito” in funzione dell’esito dell’incontro.
Caso 1) A vince 3 set a 0
Dalla formula sopra riportata si ottiene che l’ammontare punti di A è pari a: k * (risultato conseguito – risultato atteso) = 20 * (1 – 0,8) = 4 punti ; essendo il risultato della formula positivo, si tratta di 4 punti guadagnati
Volendo calcolare l’ammontare punti di B si otterrebbe che: k * (risultato conseguito – risultato atteso) = 20 * (0 – 0,2) = – 4 punti; risultato della formula negativo quindi 4 punti persi
Come spiegato sopra, il sistema ELO Coumba è perfettamente bilanciato quindi è inutile eseguire questo secondo calcolo. Se A guadagna 4 punti, automaticamente B ne perde 4.
In questo caso 1) A ha ottenuto un risultato leggermente migliore di quanto prevedibile essendo la differenza di ranking non così ampia da rendere prevedibile una vittoria così netta.
Caso 2) A vince 3 seta 1
Calcoliamo l’ammontare punti di A: k * (risultato conseguito – risultato atteso) = 20 * (0,8 – 0,8) = 0 punti
Analogamente il risultato di B è pari a 0 punti
In questo secondo caso non vi è alcune variazione di ranking fra i giocatori in quanto l’incontro è terminato esattamente secondo le rispettive percentuali di vittoria prevedibili (o risultati attesi) che avevano prima di disputare l’incontro. Quindi sostanzialmente l’incontro conferma il ranking dei due giocatori.
Caso 3) A vince 3 set a 2
Calcoliamo l’ammontare punti di A: k * (risultato conseguito – risultato atteso) = 20 * (0,6 – 0,8) = – 4 punti
Analogamente B guadagna 4 punti
In questa terza ipotesi l’incontro è stato molto bilanciato contrariamente a quanto ci si potesse aspettare in relazione ai rispettivi ranking. Quindi paradossalmente A perde dei punti pur vincendo perché il risultato atteso era una vittoria più netta di quanto effettivamente avvenuto
Caso 4) A perde 2 set a 3
Calcoliamo l’ammontare punti di A: k * (risultato conseguito – risultato atteso) = 20 * (0,4 – 0,8) = – 8 punti
Analogamente B guadagna 8 punti
Caso 5) A perde 1 set a 3
Calcoliamo l’ammontare punti di A: k * (risultato conseguito – risultato atteso) = 20 * (0,2 – 0,8) = – 12 punti
Analogamente B guadagna 12 punti
Caso 6) A perde 0 set a 3
Calcoliamo l’ammontare punti di A: k * (risultato conseguito – risultato atteso) = 20 * (0 – 0,8) = – 16 punti
Analogamente B guadagna 16 punti
Negli ultimi 3 casi A perde un incontro che avrebbe dovuto vincere secondo il suo ranking mentre B vince a sorpresa e guadagna tanti più punti quanto più nettamente riesce ad imporsi.
Il sistema coì inventato dal geniale matematico ELO, alla lunga dopo un congruo numero di partite disputate fra diversi giocatori, riesce a definire la forza relativa fra i diversi partecipanti in quanto tende a fare convergere tutti al proprio livello (o ranking) di probabilità di vittoria l’uno con l’altro.
Il caso 6) dell’esempio sta a significare che il ranking inziale dei due giocatori non era corretto relativamente alla rispettiva forza e matematicamente forza il punteggio di B a crescere molto più velocemente rispetto gli altri casi. Quando invece il risultato conseguito rispetta la probabilità di vittoria iniziale, addirittura il sistema non modifica o modifica pochissimo i rispettivi punteggi, stando a significare che la differenza di forza dei due giocatori è effettivamente pari al ranking posseduto.